MYSTERY #2
Will regulators accept a skew-adjusted approach
to application-timestamp error?
For simplicity, let’s assume for the moment that we only care about maximum divergence. I’ll extend the discussion to percentiles in a moment.
Consider System C, which has the application-level error profile of Figure 4, below. As before, suppose my budget for application-timestamp error is 40 microseconds. Figure 4 shows that the max for this platform is 61 microseconds, so clearly this platform exceeds my budget and requires remediation, right?
Timestamp Errors with Respect to Host Clock (STAC-TS.ALE1)
Worst Case Error Percentiles (microseconds)
System C
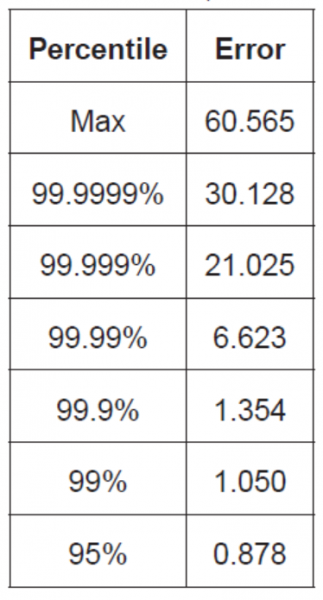
Figure 4
Not necessarily. Note that application-level error is always positive (the system can only delay access to the clock; it can’t provide a timestamp before it’s requested). But recall that the maximum divergence language of RTS 25 allows timestamps to be within some amount either side of UTC. (A maximum divergence of 100 microseconds means +/- 100 microseconds.)
Other tables (not shown) in the STAC Report for System C say that its minimum error is 0.047 microseconds—or if rounding to the nearest microsecond, 0 microseconds. So that means that I know my error will always range from a minimum of 0 to a maximum of 61 microseconds. Another way of expressing this is that the error is
30.5 +/- 30.5 microseconds
That means that for this platform, if we subtract 30.5 microseconds from every timestamp (that is, if we treat the range’s midpoint, 30.5 microseconds, as timing skew), the resulting error of those timestamps will be
0 +/- 30.5 microseconds
Voila! By treating the midpoint as timing skew, this platform is now within our error budget.
Is this some sleight of hand? Not at all. In this approach, we make a simple tradeoff. By subtracting a fixed amount from future timestamps, we magnify the error of most of those future timestamps while ensuring that all of them stay within the RTS 25 bounds.
This is absolutely within the letter of RTS 25. Is it consistent with the spirit? I honestly don’t know (which is why I consider it a mystery). While it is defensible in practical terms, ESMA may rule that deliberately making some timestamps less accurate than they could be is never acceptable, even if it means ensuring that all timestamps are sufficiently accurate.
I said above that the skew-adjustment approach can apply to percentiles as well as the max. Figure 5, taken from the STAC Report for System C, shows this. In place of percentiles, we use prediction intervals. Prediction intervals are the equivalent of percentiles applied to ranges within a distribution. They are particularly useful for distributions that have outliers on both the left and right but can also be applied to cases like application-level error, which have positive outliers only. STAC-TS uses prediction intervals to analyze many other benchmarks. I’ll explain how we derive them in a subsequent blog, but you can also read about their importance here.
Figure 5 shows the probability (first column) that the timestamp error will fall within the given range (second column) if we subtract the midpoint of the distribution (third column) from all timestamps.
Timestamp Errors with Respect to Host Clock (STAC-TS.ALE1)
Worst Case Error Prediction Intervals (microseconds)
System C
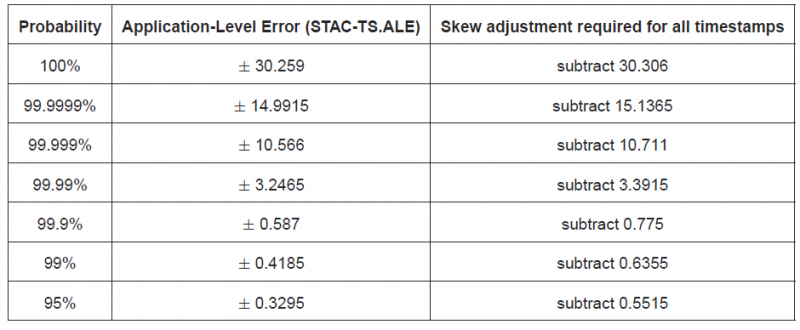
Figure 5
