MYTH #2
Application-level error isn’t significant enough to matter.
Look at how small my mean and standard deviation are.
We can establish upper bounds on application-level error by wrapping calls to the subject timestamp method in other timestamps or by calling the method repeatedly without wrapping it. These observations provide an upper bound on timestamp-assignment delay.
The mean of these observations is typically quite small—on the order of tens of nanoseconds. That is over 1000 times smaller than the error allowed by even the most stringent RTS 25 requirement of +/- 100 microseconds. Similarly, the standard deviation, a common way to measure the variability in a statistical distribution, is also the same small order of magnitude.
But many people unjustifiably use the sample mean and standard deviation to claim (for example) that 99% of the application-level errors on a given platform will be within two standard deviations of the mean. This is a misuse and misinterpretation of confidence intervals. Confidence intervals do not predict the probability that a future observation will be a given value; they indicate the strength of a hypothesis that the true mean of the distribution that is being sampled is a given value. And even that knowledge isn’t very useful, because mean timestamp error is irrelevant to RTS 25. RTS 25 is all about outliers, not averages. In fact, its wording is specifically about the maximum outlier. (How those words will get enforced is one of the mysteries that I discuss later in this blog series.) So what we need is the probability that a given timestamp will be beyond some threshold value. That is, we’re concerned with prediction.
In making those predictions, we can’t assume distributions are normal (Gaussian), either. Figure 1 is a typical example of such a distribution, displayed in a histogram with vertical and horizontal log scales to enable better scrutiny. This is from one of four test sequences that the STAC-TS.ALE tools run on a system. The system in this case is C++ using the clock_gettime() call on a default installation of Red Hat 6.9 on a server that is about four years old. This kind of system and timestamping method are not uncommon in the wild today.
Timestamp Errors with Respect to Host Clock (microseconds)
Test Sequence: STAG_REF / System A
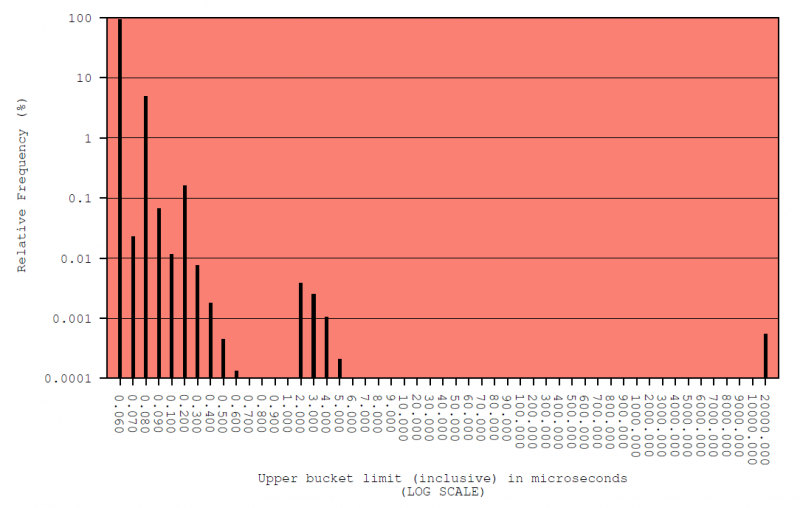
Figure 1
A quick glance makes it obvious that our observed distribution is not normal. It is bounded on the left by zero. Nearly all the observations are in the first bucket, between 50 and 60 nanoseconds (0.050 and 0.060 microseconds). The bar for that bucket stretches nearly to 100% (it is a couple percent shy but looks closer to 100% due to the log scale. And the distribution has a very long, positive tail. In other words, application-level error is characterized by a lot of positive outliers.
Consider Figure 2, which summarizes the measurements of application-level error across all four test sequences run on the system from Figure 1 (System A):
Timestamp Errors with Respect to Host Clock (STAC-TS.ALE1)
Worst Case Error Percentiles (microseconds)
System A
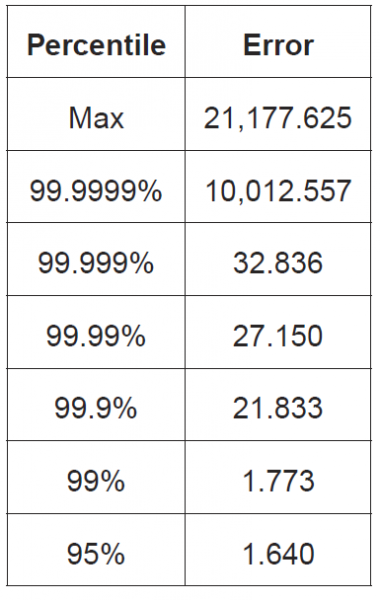
Figure 2
This table shows several percentiles, all the way up to the maximum (the 100th percentile). Percentiles are a time-honored means of characterizing a distribution’s outliers without needing to fit the distribution to some theoretical model that is described by a set of parameters (e.g., Gaussian, Poisson, gamma, etc.). That is to say, percentiles are non-parametric statistics. (In a subsequent blog, I’ll explain why non-parametric statistics are generally superior to parametric statistics for a case like RTS 25.)
Note that the maximum of 21,177 microseconds is way beyond the MiFID 2 tolerance even for non-HFT electronic trading (1 millisecond). And remember that this is just the application-level error. It doesn’t include host clock error. Even if the host clock were perfectly synchronized to UTC, some timestamps from this platform would violate RTS 25.
Faced with this kind of reality, some people carry another myth around with them….
